Supertypes and Subtypes

Subtype polymorphism pivots on the notion that a subtype fits wherever a supertype is expected. This fitting might happen in an assignment statement, like these:

Supertype item = new Subtype();

Supertype[] items = new Supertype[10];
items[0] = new Subtype();

Or in a call to a polymorphic method:

void process(Supertype item) {
  // ...
}

process(new Subtype());

Method calls invoke subtype behavior even though the compiler only knows the supertype.

Liskov Substitution

The idea that polymorphic code should be able to operate on supertype objects and subtype objects in the exact same manner has a formal name: the Liskov substitution principle. Computer scientist Barbara Liskov identified the principle in the 1980s as part of a larger effort to ground object-oriented programming on a theoretical foundation.

Another way to state the principle is that all subtypes in a hierarchy must pass the unit tests of the supertype. A subtype may add extra features, but it cannot change the interface imposed by the supertype.

The idea that subtypes may substitute for supertypes might sound unsurprising. After all, we've been writing Java code that takes full advantage of this. Any class that inherits from another can be used wherever the superclass is expected, right? For example, a square is a subtype of rectangle that happens to have sides of equal length. FileNotFoundException is a subtype of IOException that deals specifically with missing files. Dialog is a subtype of Window that specializes in small windows that focus the user's attention on a particular interaction.

Bad news. The subtype relationship is trickier to get right than you think. A square is not a true subtype of rectangle. Imagine we have this Rectangle class in a Java program:

public class Rectangle {
  private int width;
  private int height;

  public Rectangle(int width, int height) {
    setSize(width, height);
  }

  public void setSize(int width, int height) {
    this.width = width;
    this.height = height;
  }
}

This Square class extends Rectangle and offers a narrower interface:

public class Square extends Rectangle {
  public Square(int size) {
    this(size, size);
  }

  public void setSize(int size) {
    this.setSize(size, size);
  }
}

What should happen when this code is executed?

Rectangle r = new Square(6);
r.setSize(3, 7);

The square's squarishness is not maintained by this code. The square's width is set to 3 and its height is set to 7, which isn't very square. This hierarchy does not pass Liskov's requirements for the substitution principle. A Rectangle is expected to have a width independent of its height, but a Square is expected to have a uniform side length. Square should therefore not be a subtype of Rectangle, at least not when modeled in software. Square would not pass the unit tests of Rectangle.

The takeaway is that languages give us features that make it easier to write poorly designed and unsafe code. Inheritance is one of those features.

Variance

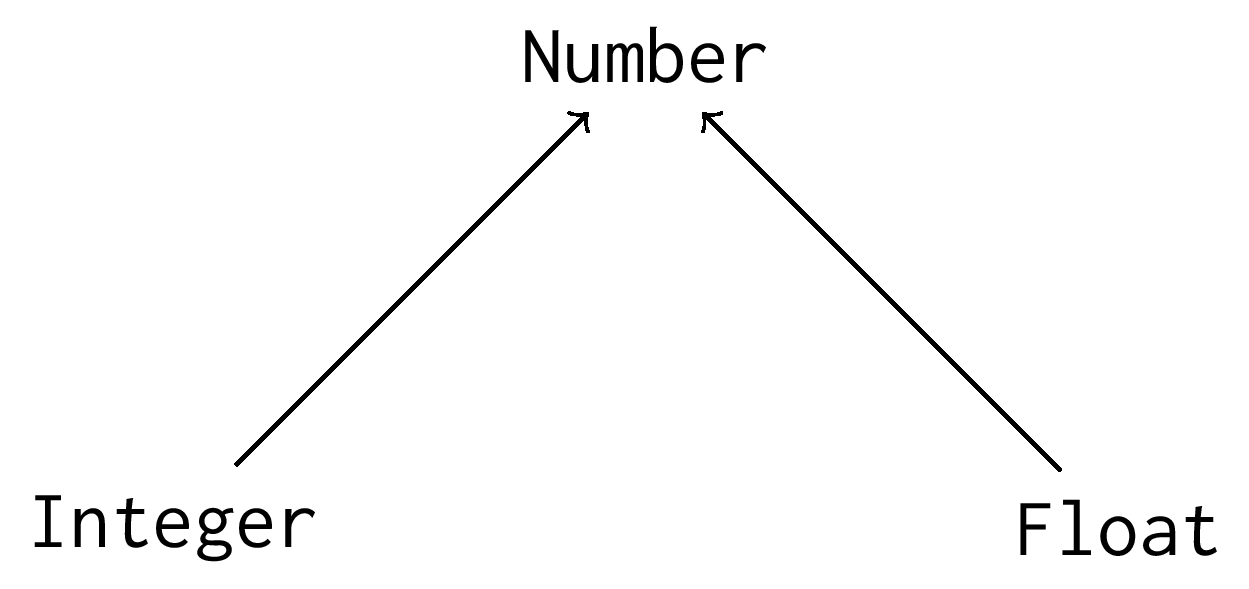
Imagine that we have a Number trait or interface and two implementing types: Integer and Float. Integer is a subtype of Number, and Float is also a subtype of Number. We can provide an Integer or a Float anywhere a Number is expected. They form this polymorphic hierarchy:

Now suppose a library method expects a List<Number>. Can we provide a List<Integer>? In other words, is List<Integer> a subtype of List<Number>? A short thought experiment tells us the answer. Suppose that List<Integer> is a subtype of List<Number>. Then we can write this assignment:

List<Number> numbers = new List<Integer>();

Oh, so we've got a List<Number>? That means we can write this code:

numbers.add(Math.PI);

Since Math.PI is a Number, the compiler gives this code the thumbs-up. But hold on. The constructed list holds integers, and this code adds to it PI, which is definitely not an integer. This inconsistency cannot be allowed. Therefore a List<Integer> cannot be considered a subtype of List<Number>. The Java compiler forbids the above assignment of List<Integer> to List<Number>.

If we want a compound type like a generic class or an array to be a subtype of another compound type, we have to respect their variance relationship. The variance of a type system dictates how component types of a compound supertype and subtype may vary. List<Integer> is not a subtype of List<Number> in Java because the List class is invariant on its type parameter T—which means that T is not allowed to vary at all. If you ask for a container of fruit, under invariance I cannot give you a container of oranges—as you might put some fruit in there that's not an orange. I can, however, give you a box of fruit or a bag of fruit. Invariance only stops the component type from varying. We can't change the invariance of component types in Java. It is a property of its type system meant to uphold the safety of compound types.

But the story of subtyping and variance is messier for arrays in Java.