Precedence

The precedence of an operator is a measure of its greediness in the mad scramble for operands. An operator with higher precedence clutches on to its operands more swiftly than one with lower precedence. Consider this expression:

a + b * c

a + b * c

Multiplication has higher precedence than addition, so * grabs onto b and c first. Then + grabs onto a and b * c.

Precedence shapes the parse tree. Lower-precedence operations build on top of higher-precedence operations, which means that higher-precedence operations will be lower in the tree. The higher-precedent multiplication is lower in this tree for a + b * c:

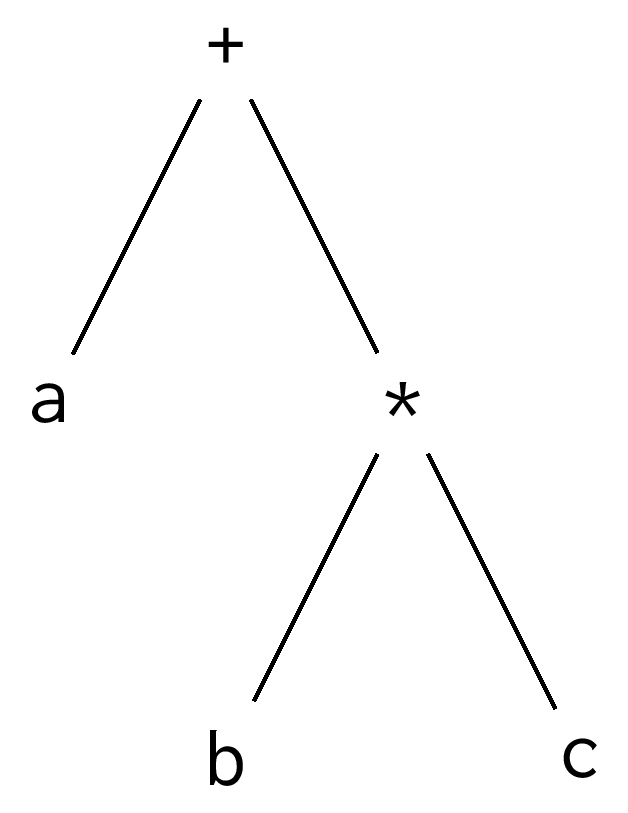
All mainstream programming languages with infix operators adhere to the precedence levels inherited from mathematical convention:

• parenthesized operations
• exponentiation
• multiplication, division, modulation
• addition, subtraction

Parentheses have the highest precedence. An operator surrounded by parentheses will be greedier than the operators outside the parentheses. In the expression (a + b) * c, the addition has higher precedence, which results in this parse tree:

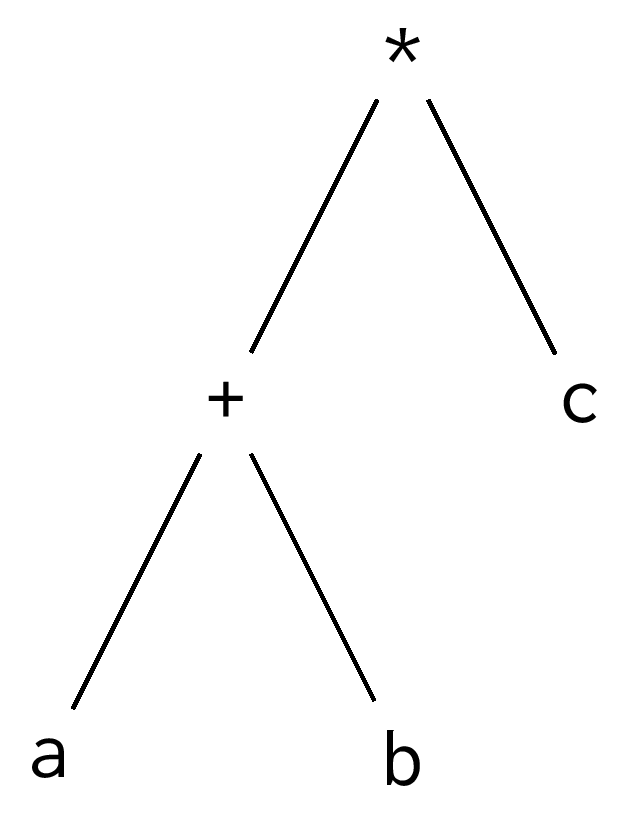
The precedences we learned in math are preserved in programming languages, but there are other, non-arithmetic operators that must be placed somewhere on the precedence spectrum. Operators like ~, <<, and & don't have the advantage of centuries of convention justifying their ranking.

Generally, operators are ordered into precedence levels so as to minimize the number of parentheses needed to steer the parsing. The following precedence rules are obeyed by most languages:

• The member and subscript operators have highest precedence. If they didn't, the expression 1 + numbers.size would parse as (1 + numbers).size instead of 1 + (numbers.size).
• The unary operators have the next highest precedence. If they had higher precedence, then the expression -offsets[0] would parse as (-offsets)[0] instead of -(offsets[0]).
• The equality and relational operators have lower precedence than the additive operators. Otherwise, the expression i + 1 > 6 would parse as i + (1 > 6) instead of (i + 1) > 6.
• The logical operators have lower precedence than the relational operators. Otherwise, the expression x > 0 && y > 0 would parse as x > (0 && y) > 0 instead of (x > 0) && (y > 0).
• The assignment operators have the least precedence. Otherwise, the expression big = i > 100 would parse as (big = i) > 100 instead of big = (i > 100).

The precedence of an operator is sometimes baked into the language's grammar. Consider this grammar that allows expressions like 5 + 6 * 7 and angle / 180 * pi + pi / 2:

expression
  = additive

additive
  = additive PLUS multiplicative
  | additive MINUS multiplicative
  | multiplicative

multiplicative
  = multiplicative ASTERISK atom
  | multiplicative SLASH atom
  | atom

atom
  = INTEGER
  | IDENTIFIER
  | ( expression )

expression
  = additive

additive
  = additive PLUS multiplicative
  | additive MINUS multiplicative
  | multiplicative

multiplicative
  = multiplicative ASTERISK atom
  | multiplicative SLASH atom
  | atom

atom
  = INTEGER
  | IDENTIFIER
  | ( expression )

An operator's precedence level is effectively the number of productions that need to be applied to get from the starting non-terminal to the operator. The + and - operators are both one production away, so they form precedence level 1. The * and / operators are both two productions away, so they form precedence level 2. Parentheses are three productions away, so they have the highest precedence.

The numeric precedence levels are never actually considered or compared, at least not in the recursive descent parsing algorithm modeled off this grammar. The productions themselves ensure that multiplicative operators appear lower in the parse tree, and that placement is what gives the multiplicative operators higher precedence.

Overriding Precedence

Sometimes we want to override the precedence of operators. Often we achieve this with parentheses. As we saw above, to make the addition happen first in a + b * c, we write (a + b) * c. Parentheses trigger the parser into making an abstract syntax tree node for the expression within, effectively giving the expression higher precedence than everything else around it.

Haskell provides another mechanism for influencing precedence. Suppose we have a list of words, and we want to find the length of the first word. We might try writing this expression:

length head words

length head words

This fails because function calling has higher precedence than anything else in Haskell, and it's left-associative. The expression parses as (length head) words. The parser sees the length function getting called first, and length receives the uncalled head function as its only parameter. We can fix this with parentheses:

length (head words)

length (head words)

The parentheses force the parser to make a tree node for head words. But we can also fix this with Haskell's function application operator $:

length $ head words

length $ head words

All that the $ operator does is pass the value on its right as a parameter to the function on its left. At first blush, that sounds utterly useless. We can pass parameters to functions perfectly fine without $ just by listing them in the call.

The redeeming quality of $ is not what it does, but that it has the absolute lowest precedence in the language. The expressions on either side of $ automatically have higher precedence and will get their abstract syntax tree nodes formed separately. The parser will make a node out of everything to the left of $ and a separate node out of everything to the right. It has the same effect as parenthesizing the two operand expressions.

Haskell programmers tend to favor $ over parentheses because it's less noisy and it creates a clear pipeline of computation that gets evaluated linearly from right to left. Suppose we need to pass the value x through a chain of five functions. With parentheses, we'd write:

f (g (h (i (j x))))

f (g (h (i (j x))))

With $, we'd write:

f $ g $ h $ i $ j x

f $ g $ h $ i $ j x

By character count, the code isn't shorter with $. However, there are fewer parentheses to fight.