Operators

Operators are the special symbols that we use to compactly notate calculations. The data to which operators are applied are operands, which may be literals, variables, or function calls—any expression really. An operator and its operands form an operation.

How an operation is formed and evaluated depends on these four properties:

1. arity, or the number of operands
2. fixity, or the placement of the operator
3. precedence
4. associativity

We examine each of these properties in turn.

Arity

Earlier we learned that arity is the number of parameters that a function expects. It is also used to describe the number of operands an operator expects. Most languages have a few unary operators, many binary operators, and maybe a single ternary operator.

A unary operator has only a single operand. The only unary operator in Haskell is the arithmetic negation operator -. Other languages provide more, including the logical negation operators ! and not, the bitwise negation operator ~, the sizeof operator, the address-of operator &, the dereference operator *, and the increment and decrement operators ++ and --.

Some languages provide the unary + operator to complement the - operator. In many circumstances, this operator performs an identity operation, yielding the value of its operand. However, it usually has the extra semantics of converting types. In C, +x converts x to an int. In JavaScript, unary + can be used to turn non-numbers into numbers:

console.log(+true);      // prints 1
console.log(+false);     // prints 0
console.log('53' + 2);   // prints 532
console.log(+'53' + 2);  // prints 55
console.log(+'76ers');   // prints NaN

Haskell does not have unary +. But it does have an id function that accepts a single parameter:

id 99        -- yields 99
id "snurb"   -- yields "snurb"

Imagining a use for the id function is hard. But one may arise as we use higher-order functions.

A binary operator has two operands. Typical binary operators include the arithmetic operators +, -, *, /, and %; the relational operators <, <=, >, and >=; the equality operators ==, !=, /=, and <>; the logical operators &&, ||, and, and or; the subscript operator []; the bitwise operators <<, >>, and ^; the member operators -> and .; and the assignment operators =, +=, *=, and so on.

Haskell has a unique take on some of these binary operators. For instance, there is no % operator defined in the standard library, which is called the Prelude. Additionally, it doesn't have any of the compound assignment operators like +=. In C, += and its cousins are really two operations in one:

x += 1;    // effectively expands to x = x + 1

The left operand is first treated as an rvalue to perform the + operation. Then it is treated as an lvalue to perform the assignment. Haskell doesn't allow mutation, and these compound operators are therefore omitted from the language. There are named bitwise functions like shiftL, but not bitwise operators. The subscript operator is !!, and it is used like this:

"#FC621D" !! 6    -- yields 'D'

The whole linked list must be traversed to reach that 'D'. Use !! sparingly.

Ruby provides the rocketship operator <=>, which is used to order its operands:

91 <=> 93       # yields -1
91 <=> 91       # yields 0
93 <=> 91       # yields 1

Java provides similar behavior to the rocketship operator through its compareTo methods:

Integer x = 91;
Integer y = 93;
x.compareTo(y)  // yields value < 0
x.compareTo(x)  // yields 0
y.compareTo(x)  // yields value > 0

Haskell provides a compare function rather than an operator:

compare 91 93   -- yields LT
compare 91 91   -- yields EQ
compare 93 91   -- yields GT

A ternary operator has three operands. Most languages have just one ternary operator: the conditional expression. In the C family of languages and in Ruby, it has this syntax:

legClothes = temperature > 25 ? "shorts" : "pants";

This operator branches like an if statement, but instead of achieving some side-effect, it chooses between its then and else expressions, yielding the selected value. Haskell's conditional expression has this form:

legClothes = if temperature > 25 then "shorts" else "pants"

Haskell has no conditional statement. If there's an if, it's a value-producing expression. We may write it with linebreaks, but it's still an expression:

legClothes =
  if temperature > 25
    then "shorts"
    else "pants"

In imperative languages the else branch of a conditional statement may be omitted if there's nothing to do when the condition is false. That's not legal in Haskell's conditional expression. A value must always be produced, so the else branch must be present. Additionally, the branches must produce values of the same type.

Sometimes mathematicians and novice programmers long for a ternary interval operator so that they can write code like 0 <= x <= 100. Alas, most mainstream languages treat this as two binary operations. The first, 0 <= x, yields a boolean value, and the second confusingly compares the boolean to 100, which probably isn't the behavior we want and may not typecheck. Python is a notable exception. Its parser recognizes chains like 0 <= x <= 100 and evaluates them according to our mathematical expectations.

Fixity

Operators are placed near their operands in three common ways. Prefix operators appear before their operand, postfix operators appear after their operand, and infix operators appear between their operands, as shown here for operator @ and operands x and y:

@x      <- prefix
x@      <- postfix
x @ y   <- infix

An operator's placement is also called its fixity.

Most binary and ternary operators are infix operators, and most unary operators are prefix operators. However, the increment operator ++ and decrement operator -- have both prefix and postfix forms in languages with mutability. They both increment and yield a value, but they differ in the order in which these happen. Their placement determines the order:

let x = 1;
let y = 1;
console.log(x++);  // post-increment: yield 1, assign x = 2
console.log(++y);  // pre-increment: assign y = 2, yield 2

The prefix form ++y puts the ++ first, reflecting that the increment has priority. The value of the expression is the incremented number. The postfix form x++ puts the x first, reflecting that the unincremented value of x has priority. The value of the expression is the unincremented value of x. These operators yield different values according to their fixity. If we never embed these operations in a larger expression that consumes the yielded value, their differences don't really matter.

The increment and decrement operators are not present in Haskell. Nor in Ruby or Python. These operators are often used to update indices in count-controlled for loops in the C family of languages. Ruby and Python do not have these loops, favoring range-based and for-each loops, so the operators are less useful. The more general binary operators += and -= are available in Python and Ruby.

Haskell's binary operators can be either prefix or infix. In prefix form, they must be parenthesized:

5 + 6     -- yields 11
(+) 5 6   -- yields 11

You are probably wondering why you would ever want the prefix form. That is a reasonable question that we will address when we discuss a feature called partial function application in a later chapter.

Interestingly, Haskell operators and functions are more or less the same thing. Consider the div function, which is used to perform integer division. Usually, function names appear in a prefix position, but Haskell lets us treat them as an infix operator using backticks:

div 16 5      -- yields 3
16 `div` 5    -- yields 3

The only difference between an operator and a function in Haskell is that an operator defaults to having infix placement, while a function defaults to having prefix placement.

The Haskell lexer decides what is an operator and what is a function by examining the characters in their tokens. A function is made of alphanumeric characters and an operator is made of punctuation.

The Lisp family of languages uses prefix operators exclusively. One benefit of this form is that operators that are normally binary naturally become variadic:

(+ 1 2)       ; yields 3
(+ 1 2 3 4)   ; yields 10

Precedence

The precedence of an operator is a measure of its greediness in the mad scramble for operands. An operator with higher precedence clutches on to its operands more swiftly than one with lower precedence. Consider this expression:

a + b * c

Multiplication has higher precedence than addition, so * grabs onto b and c first. Then + grabs onto a and b * c.

Precedence shapes the parse tree. Lower-precedence operations build on top of higher-precedence operations, which means that higher-precedence operations will be lower in the tree. The higher-precedent multiplication is lower in this tree for a + b * c:

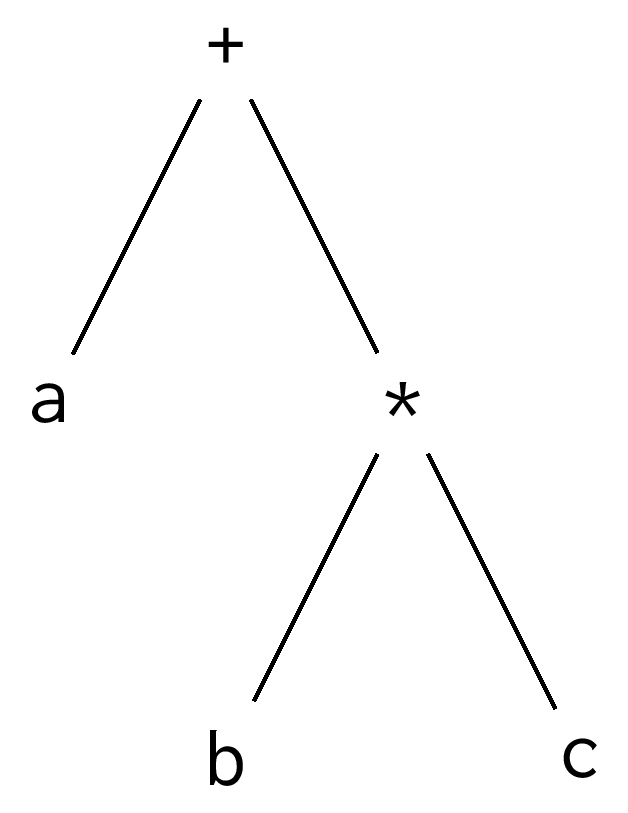
All mainstream programming languages with infix operators adhere to the precedence levels inherited from mathematical convention:

• parenthesized operations
• exponentiation
• multiplication, division, modulation
• addition, subtraction

Parentheses have the highest precedence. An operator surrounded by parentheses will be greedier than the operators outside the parentheses. In the expression (a + b) * c, the addition has higher precedence, which results in this parse tree:

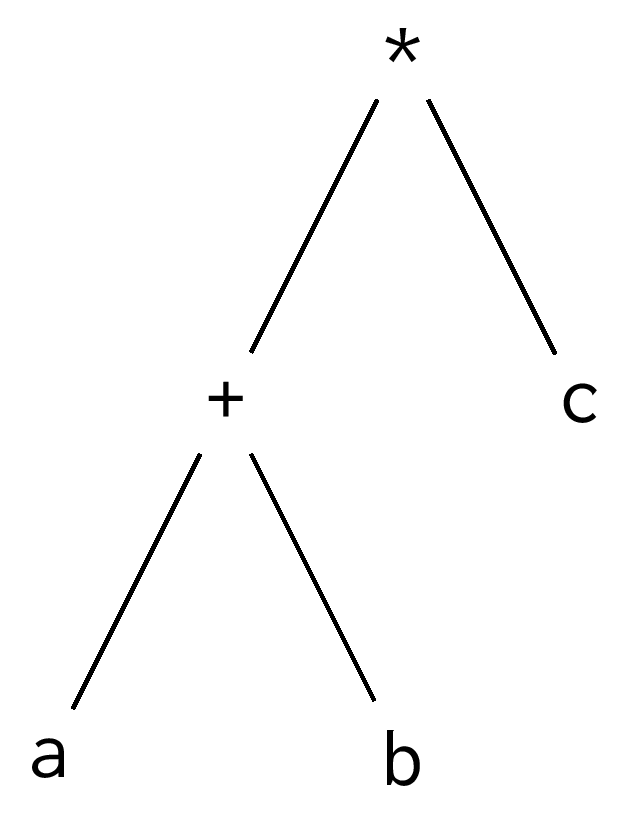
The precedences we learned in math are preserved in programming languages, but there are other, non-arithmetic operators that must be placed somewhere on the precedence spectrum. Operators like ~, <<, and & don't have the advantage of centuries of convention justifying their ranking.

Generally, operators are ordered into precedence levels so as to minimize the number of parentheses needed to steer the parsing. The following precedence rules are obeyed by most languages:

• The member and subscript operators have highest precedence. If they didn't, the expression 1 + numbers.size would parse as (1 + numbers).size instead of 1 + (numbers.size).
• The unary operators have the next highest precedence. If they had higher precedence, then the expression -offsets[0] would parse as (-offsets)[0] instead of -(offsets[0]).
• The equality and relational operators have lower precedence than the additive operators. Otherwise, the expression i + 1 > 6 would parse as i + (1 > 6) instead of (i + 1) > 6.
• The logical operators have lower precedence than the relational operators. Otherwise, the expression x > 0 && y > 0 would parse as x > (0 && y) > 0 instead of (x > 0) && (y > 0).
• The assignment operators have the least precedence. Otherwise, the expression big = i > 100 would parse as (big = i) > 100 instead of big = (i > 100).

The precedence of an operator is sometimes baked into the language's grammar. Consider this grammar that allows expressions like 5 + 6 * 7 and angle / 180 * pi + pi / 2:

expression
  = additive

additive
  = additive PLUS multiplicative
  | additive MINUS multiplicative
  | multiplicative

multiplicative
  = multiplicative ASTERISK atom
  | multiplicative SLASH atom
  | atom

atom
  = INTEGER
  | IDENTIFIER
  | ( expression )

An operator's precedence level is effectively the number of productions that need to be applied to get from the starting non-terminal to the operator. The + and - operators are both one production away, so they form precedence level 1. The * and / operators are both two productions away, so they form precedence level 2. Parentheses are three productions away, so they have the highest precedence.

The numeric precedence levels are never actually considered or compared, at least not in the recursive descent parsing algorithm modeled off this grammar. The productions themselves ensure that multiplicative operators appear lower in the parse tree, and that placement is what gives the multiplicative operators higher precedence.

Associativity

Suppose we have the expression 5 - 3 + 2. Should it parse as 5 - (3 + 2) or (5 - 3) + 2? Does it matter which way it parses?

The parsing order does matter. Precedence tells us that + is just as greedy as -, so it's no help here. To break precedence ties, we examine the associativity of the operators. Mathematical convention says the additive operators + and - are left-associative, which means whichever operator is leftmost is greediest. For this expression, the - operator is leftmost and is the greediest. It will appear lower in the parse tree.

The vast majority of operators are left-associative, but there are a few exceptions. By mathematical convention, exponentiation is right-associative, which means whichever operator is rightmost is greediest.

The assignment operators are also right-associative. Assignment operators can only match precedence with other assignment operators since they are the only operators at their precedence level. Therefore, their associativity only matters when an expression contains multiple assignment operators, as in a = b = 8. This parses as a = (b = 8). Both a and b end up bound to 8.

Haskell doesn't treat assignment as an expression and doesn't support chained assignments. The associativity of = is irrelevant in Haskell.

In the Lisp family of languages, associativity is unimportant, since each operation is explicitly surrounded by parentheses, as shown in this Racket expression:

(+ (- 5 3) 2)

As with precedence, an operator's associativity is an artifact of the grammar. This non-terminal recurses in its left operand:

additive 
  = additive PLUS multiplicative
  | additive MINUS multiplicative
  | multiplicative

Because the recursion happens on the left, the leftmost + or - will be lowest in the tree, making these operators left-associative. The production for a right-associative operator will recurse in its right operand.