Fall 2024 Rust Exam

Problem 1

Write function opposite that accepts two parameters: a point A and a point B. Each is an xy-coordinate pair—a 2-tuple of f64. It returns a point C that is like B but in the opposite direction from A. For example:

Problem 2

Write a main that accepts two unsigned integers as command-line arguments. It prints the equations of six arithmetic operations on the two numbers. For example:

Shell
$ ./main 3 5
3 + 5 = 8
3 - 5 = -2
3 * 5 = 15
3 / 5 = 0
3 % 5 = 3
3 ^ 5 = 243
$ ./main 3 5
3 + 5 = 8
3 - 5 = -2
3 * 5 = 15
3 / 5 = 0
3 % 5 = 3
3 ^ 5 = 243

Problem 3

Define the type Record as a struct containing a String name and a u32 score. Have the compiler automatically implement the Debug trait.

Write function rank that accepts two parameters: a borrowed Vec of Record, and a name as a borrowed string slice. It returns the named individual's rank amongst all the records as an Option<usize>. The person with the highest score has rank 1. For example, suppose we have this vector of records:

Rust
let records = vec![
  Record {name: "Elsif", score: 44},
  Record {name: "Finny", score: 43},
  Record {name: "Grada", score: 62}
];
let records = vec![
  Record {name: "Elsif", score: 44},
  Record {name: "Finny", score: 43},
  Record {name: "Grada", score: 62}
];

Then we expect these results:

Problem 4

Imagine a game called Danger Farm played on a board of arbitrary width and height. In the bottommost row (row 0), there are 5 tiles of wheat on the left. In the next row (row 1), there are 5 tiles of wheat on the right. The wheat alternates between left and right for all remaining rows. Thistles cover the rest of the board. Any tile outside of the board is lava. Assume the board is at least 5 tiles wide. For example, here is a 12×5 board situated in some lava:

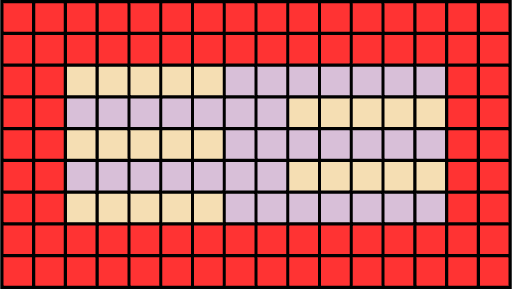
Write an enum Tile with variants Wheat, Thistle, Lava. Have the compiler automatically implement the Debug, Eq, and PartialEq traits.

Write a function hit that accepts two parameters: a board width and height as a pair of i32, and a tile column and row as a pair of i32. It returns the tile's type. For example:

Problem 5

A person's name is on several waiting lists. You want to know their best (minimal) position. Write function mindex that accepts two parameters: a borrowed Vec of waiting lists, and a name. Each name is a borrowed string slice, and each waiting list is a Vec of names. Return an Option<usize> indicating the index of the named individual's best position across all waiting lists. Suppose we have these waiting lists:

Rust
let lists = vec![
  vec!["Joël", "Paola", "Buzz"],
  vec!["Sally", "Buzz", "Paola", "Deanzel"],
  vec!["Isaida", "Claire", "Joël"],
];
let lists = vec![
  vec!["Joël", "Paola", "Buzz"],
  vec!["Sally", "Buzz", "Paola", "Deanzel"],
  vec!["Isaida", "Claire", "Joël"],
];

Then we have these minimal indices:

Use iterators and higher-order functions. The Iterator.position method is useful. Do not use loops.

Problem 6

Each subject in a taste test has sampled and scored \(n\) different foods. You want to decide how far two subjects are from one another. Write ndiff that accepts two borrowed Vec of food scores. Each score is a u32. Return the sum of the absolute differences between corresponding scores. For example:

The u32::abs_diff method is useful.

Problem 7

Write function to_ol that accepts a borrowed Vec of elements that implement the Display trait. It returns as a String the HTML form of the list. For example:

Each line ends in a linebreak.

Problem 8

A trie is a tree data structure that efficiently stores strings with common prefixes. For example, this trie represents the words dust, duck, and do:

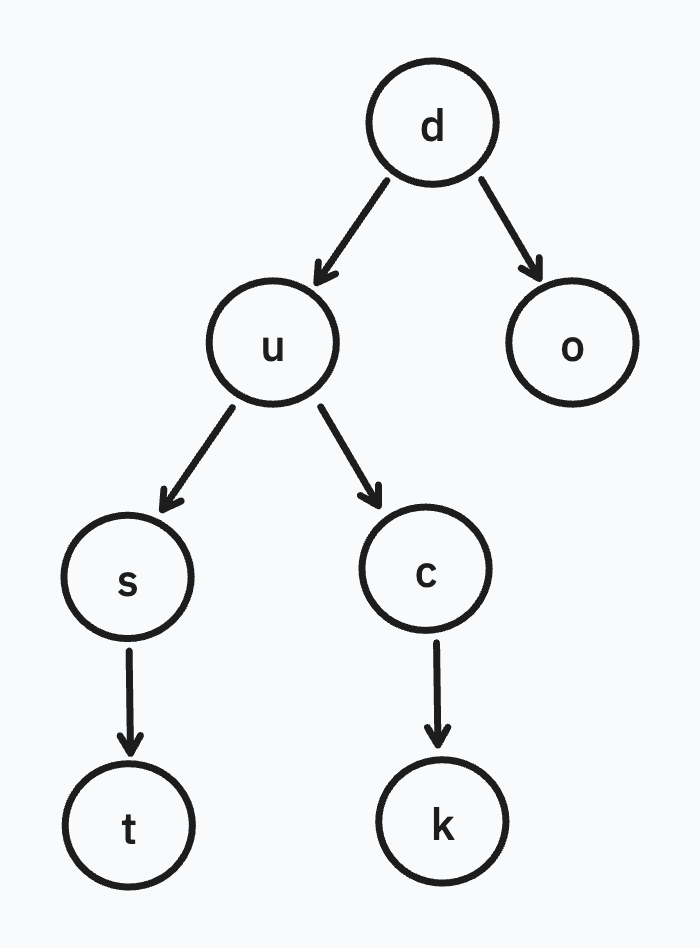
Each leaf node, prefixed by its ancestor letters, represents a word.

Your task is to model the nodes of a trie. Define a struct named Node that has these two fields:

Implement these three subroutines for Node: